This is a series of math problems from Madoka Magica Episode 1. Although these problems appeared in a middle school math lesson, they are actually pretty challenging for probably even high schoolers. There are more problems in the show, which will be covered in another blog.
Question 1: (Image from Puella Magi Wiki)

Simplified statement:
Given \(a \equiv 6 \pmod{14} \) and \(b \equiv 1 \pmod{14} \), find the remainder of \(x\) when divided by 14, given \(x\) is an integer solution to \(x^2 - 2ax + b = 0\).
Given \(a \equiv 6 \pmod{14} \) and \(b \equiv 1 \pmod{14} \), find the remainder of \(x\) when divided by 14, given \(x\) is an integer solution to \(x^2 - 2ax + b = 0\).
Solution:
By performing modular arithmetic to the quadratic equation,
\begin{align} x^2 - 2ax + b & \equiv 0 \pmod{14} \\ & \equiv x^2 - 12x + 1 \pmod{14} \\ & \equiv x^2 - 12x + 14x + 1 \pmod{14} \\ & \equiv x^2 + 2x + 1 \pmod{14} \\ & \equiv (x + 1)^2 \pmod{14} \\ & \equiv x + 1 \pmod{14} \end{align} Therefore, \(x \equiv 13 \pmod{14}\)
By performing modular arithmetic to the quadratic equation,
\begin{align} x^2 - 2ax + b & \equiv 0 \pmod{14} \\ & \equiv x^2 - 12x + 1 \pmod{14} \\ & \equiv x^2 - 12x + 14x + 1 \pmod{14} \\ & \equiv x^2 + 2x + 1 \pmod{14} \\ & \equiv (x + 1)^2 \pmod{14} \\ & \equiv x + 1 \pmod{14} \end{align} Therefore, \(x \equiv 13 \pmod{14}\)
Question 2: (Image from Puella Magi Wiki)

Statement:
Suppose \(p\) is a prime number and \(n\) is an arbitrary natural number, prove that \((1 + n)^p - n^p - 1\) is divisible by \(p\).
Suppose \(p\) is a prime number and \(n\) is an arbitrary natural number, prove that \((1 + n)^p - n^p - 1\) is divisible by \(p\).
Solution:
This is a good place to use Fermat's Little Theorem:
This is a good place to use Fermat's Little Theorem:
Fermat's Little Theorem:
For any prime \(p\) and integer \(a\), we have $$ a^p \equiv a \pmod{p} $$
\((1 + n)^p - n^p - 1 \equiv (1 + n) - n - 1 \equiv 0 \pmod{p}\)
For any prime \(p\) and integer \(a\), we have $$ a^p \equiv a \pmod{p} $$
Question 3: (Image from Puella Magi Wiki)

(No higher resolution image available)
Statement:
Find all integral solutions \((a, b)\) such that $$ (a^3 + a^2 - 1) = (a - 1)b $$
Statement:
Find all integral solutions \((a, b)\) such that $$ (a^3 + a^2 - 1) = (a - 1)b $$
Solution:
$$ (a^3 + a^2 - 1) = (a - 1)b $$ $$ (a^3 + a^2 - 1) - (a - 1)b = 0 $$ $$ (a^3 + a^2 - 2) - (a - 1)b = -1 $$ $$ (a - 1)(a^2 + 2a + 2) - (a - 1)b = -1 $$ $$ (a - 1)(a^2 + 2a + 2 - b) = -1 $$ \begin{cases} a - 1 = 1 \\ a^2 + 2a + 2 - b = -1 \end{cases} or \begin{cases} a - 1 = -1 \\ a^2 + 2a + 2 - b = 1 \end{cases} Thus, we have \((a, b) = (2, 11)\) or \((0, 1)\).
$$ (a^3 + a^2 - 1) = (a - 1)b $$ $$ (a^3 + a^2 - 1) - (a - 1)b = 0 $$ $$ (a^3 + a^2 - 2) - (a - 1)b = -1 $$ $$ (a - 1)(a^2 + 2a + 2) - (a - 1)b = -1 $$ $$ (a - 1)(a^2 + 2a + 2 - b) = -1 $$ \begin{cases} a - 1 = 1 \\ a^2 + 2a + 2 - b = -1 \end{cases} or \begin{cases} a - 1 = -1 \\ a^2 + 2a + 2 - b = 1 \end{cases} Thus, we have \((a, b) = (2, 11)\) or \((0, 1)\).
Question 4: (Image from Puella Magi Wiki)
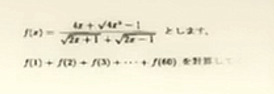
(No higher resolution image available)
Statement:
Given that $$ F(x) = \frac{4x + \sqrt{4x^2 - 1}}{\sqrt{2x + 1} + \sqrt{2x - 1}} $$ Find \(\sum_{i=1}^{60} F(i)\).
Statement:
Given that $$ F(x) = \frac{4x + \sqrt{4x^2 - 1}}{\sqrt{2x + 1} + \sqrt{2x - 1}} $$ Find \(\sum_{i=1}^{60} F(i)\).
Solution:
\begin{align} F(x) & = \frac{4x + \sqrt{4x^2 - 1}}{\sqrt{2x + 1} + \sqrt{2x - 1}} \\ & = \frac{(4x + \sqrt{4x^2 - 1})(\sqrt{2x + 1} - \sqrt{2x - 1})}{2} \\ & = \frac{(4x + \sqrt{(2x + 1)(2x - 1)})(\sqrt{2x + 1} - \sqrt{2x - 1})}{2} \\ & = \frac{(4x - 2x + 1) \sqrt{2x + 1} + (-4x + 2x + 1) \sqrt{2x - 1}}{2} \\ & = (x + \frac{1}{2}) \sqrt{2x + 1} + (\frac{1}{2} - x) \sqrt{2x - 1} \\ & = \frac{(2x + 1)^{3/2}}{2} - \frac{(2x - 1)^{3/2}}{2} \end{align} Notice that this is a telescoping series, so \begin{align} \sum_{i=1}^{60} F(i) & = \frac{1}{2} \sum_{i=1}^{60} (2i + 1)^{3/2} - (2i - 1)^{3/2} \\ & = \frac{1}{2} (121^{3/2} - 1^{3/2}) \\ & = \frac{1}{2} (1331 - 1) \\ & = 665 \end{align}
\begin{align} F(x) & = \frac{4x + \sqrt{4x^2 - 1}}{\sqrt{2x + 1} + \sqrt{2x - 1}} \\ & = \frac{(4x + \sqrt{4x^2 - 1})(\sqrt{2x + 1} - \sqrt{2x - 1})}{2} \\ & = \frac{(4x + \sqrt{(2x + 1)(2x - 1)})(\sqrt{2x + 1} - \sqrt{2x - 1})}{2} \\ & = \frac{(4x - 2x + 1) \sqrt{2x + 1} + (-4x + 2x + 1) \sqrt{2x - 1}}{2} \\ & = (x + \frac{1}{2}) \sqrt{2x + 1} + (\frac{1}{2} - x) \sqrt{2x - 1} \\ & = \frac{(2x + 1)^{3/2}}{2} - \frac{(2x - 1)^{3/2}}{2} \end{align} Notice that this is a telescoping series, so \begin{align} \sum_{i=1}^{60} F(i) & = \frac{1}{2} \sum_{i=1}^{60} (2i + 1)^{3/2} - (2i - 1)^{3/2} \\ & = \frac{1}{2} (121^{3/2} - 1^{3/2}) \\ & = \frac{1}{2} (1331 - 1) \\ & = 665 \end{align}
